improvement of gas-turbine engine dynamic structure with rotor rubbing through mathematical simulation
M.K.Leontiev and S.L.Zvonarev, Aircraft Engine Department,
Moscow Aviation Institute,
Moscow, Russia
- ABSTRACT
- INTRODUCTION
- DYNAMIC CHARACTERISTICS OF GTE MODEL
- DESIGNING OF HYDRODYNAMIC DAMPER OF INTERMEDIATE SUPPORT
- LITERATURE
ABSTRACT
The cases of rubs between the low pressure turbine rotor (LPT) and middle pressure turbine rotor (MPT) occurred in a number of the operating gas turbine engines. Initially it was stated that the reason for rotor-to-rotor rubs is temperature unbalance because of unequal cooling of LPT rotor long shaft on engines repeated by set into operation after a short time break. Both the equalizations of temperature field and the increase of the clearance between shafts did not remove this defect to the full.
To understand better the engine nature investigations of dynamic structure have been made using a program code "DYNAMICS" both in the linear and nonlinear approach.
The results obtained showed that there are two basic reasons for rotor-to-rotor rubs when there is temperature unbalance. Under some conditions the origin of LPT shape mode takes place with big deflections in the operating range. In a number of cases this resonance regime is not controlled by the intermediate support damper because of unstable damper dynamic characteristics.
The investigations allowed to determine optimal stiffness and damping characteristics to further suggest the structure of damper that does not allow rubs when temperatures unbalance is occurs.
INTRODUCTION
The use of methods of mathematical simulation for dynamic response of aircraft gas-turbine engines (GTE) is an effective way in the development of engines with optimal vibration characteristics [1]. The article presents an experience gained in engine development using such methods.
In operation some three shaft gas-turbine engines displayed contacts between the low pressure (LP) rotor and the middle pressure turbine rotor. In every case the effect was accompanied by vibrations of high level of the front support in the LP rotor - over 100 mm/s. The contacts occurred in the range of operating speeds 4700...5300 rpm on the LP rotor at the conditions of its forward synchronous whirl. It was found that rubs were caused by the increased temperature unbalance of the LP rotor because of unequal cooling of LP rotor long shaft on engines repeated by set into operation after a short time break.
Both the equalizations of temperature field and the increase of a clearance between shafts did not remove this defect to the full.
The study of the engine dynamic response through mathematical simulation enabled us to understand deeper the properties of its dynamic structure and define conditions under which the rubs can take place.
DYNAMIC CHARACTERISTICS OF GTE MODEL
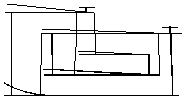
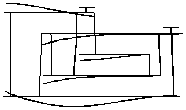
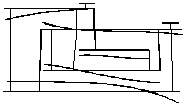
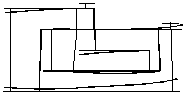
The engine has a dynamic structure consisting of a low pressure (LP) rotor, a high pressure (HP) rotor and a middle pressure (MP) rotor, a gas generator case (GG), a compressor case and outer case with an afterburner and a nozzle, Fig.1.
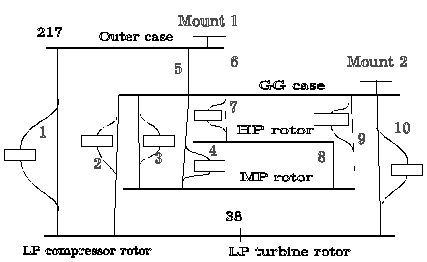
Fig. 1 Line diagram for the gas turbine engine model
In operating range of LP rotor there are six critical speeds of LP rotor and corresponding mode shapes of GTE dynamic structure, Fig 2.
|
N1=1082 rpm |
N2=2776 rpm |
N3=3404 rpm |
|
|
|
|
|
N4=3882 rpm |
N5=4345 rpm |
N6=5173 rpm |
|
|
|
|
The second, fourth and fifth mode shapes are strongly identified with resonance zones gained in experiments, Table 1.
Table 1
|
Frequency |
Resonance zone, rpm | ||
|
LP rotor |
2800...2900 |
3800...3900 |
4250...4500 |
The resonance zones corresponding to the sixth mode shape have not been registered in experiments.
The analysis results of some mode shapes are given through the vibration energy distribution, Table 2.
Table 2
|
Critical speed, rpm |
1082 |
2776 |
3404 |
3882 |
4345 |
5173 | |
|
|
LP rotor |
20.25 |
7.50 |
1.75 |
3.21 |
16.62 |
57.99 |
|
Strain energy of |
MP rotor |
0.20 |
0.52 |
2.22 |
0.23 |
1.64 |
0.71 |
|
subsystems, % |
HP rotor |
0.01 |
2.13 |
4.24 |
2.31 |
1.21 |
0.36 |
|
|
GG case |
6.69 |
2.52 |
23.83 |
7.28 |
2.60 |
1.16 |
|
|
Outer case |
15.72 |
47.68 |
0.19 |
0.66 |
13.18 |
7.87 |
|
|
1 |
0.30 |
10.25 |
16.38 |
3.53 |
36.22 |
2.71 |
|
|
2 |
7.08 |
1.94 |
6.16 |
6.63 |
9.20 |
20.33 |
|
|
3 |
0.00 |
0.23 |
0.06 |
0.02 |
1.58 |
1.44 |
|
Strain energy |
4 |
0.08 |
1.31 |
0.00 |
0.10 |
1.21 |
0.82 |
|
of links, % |
5 |
12.71 |
20.20 |
1.82 |
0.01 |
0.56 |
0.26 |
|
|
6 |
36.74 |
0.07 |
1.22 |
0.05 |
0.17 |
0.23 |
|
|
7 |
0.01 |
8.08 |
18.19 |
9.40 |
5.37 |
12.60 |
|
|
8 |
0.00 |
0.25 |
0.87 |
0.22 |
0.40 |
0.14 |
|
|
9 |
0.00 |
2.65 |
13.22 |
1.67 |
7.66 |
2.62 |
|
|
10 |
0.18 |
0.60 |
9.80 |
64.63 |
2.31 |
1.72 |
|
|
LP rotor |
33.50 |
18.46 |
35.32 |
82.28 |
44.58 |
76.38 |
|
|
MP rotor |
0.93 |
10.67 |
8.24 |
0.32 |
15.41 |
7.16 |
|
Kinetic energy |
HP rotor |
0.36 |
23.79 |
39.63 |
13.60 |
9.37 |
2.21 |
|
of subsystems |
GG case |
2.02 |
17.27 |
6.63 |
2.35 |
13.44 |
5.69 |
|
|
Outer case |
63.19 |
29.82 |
10.18 |
1.44 |
17.20 |
8.57 |
Mode 2776 rpm. Over 18 % of kinetic energy of LP rotor and considerable deformation of the front support (over 10% of strain energy) certify that this form will display vibrations on the front support of the LP rotor.
Mode 3882 rpm. This mode can display with the frequency of LP rotor (over 82% of kinetic energy). The rear support of LP rotor has large deformation (64% of strain energy). It is possible to control the mode by installing a damper in the rear support.
Mode 4345 rpm. The mode is intensively excited with the frequency of LP rotor (over 44% of kinetic and 16% of strain energy). It will display a high level of vibrations of the front support of LP rotor (36% of strain energy). The mode can be effectively controlled by a damper in the front support of LP rotor.
Mode 5173 rpm. The mode of bending vibrations of the LP rotor (over 57% of strain energy). It is intensively excited with the frequency of LP rotor (over 76% of kinetic energy). It can act with greater bending of the LP rotor. It is possible to control the mode by adjusting a damping device in the intermediate support of LP rotor (over 20% of total strain energy)
The steady state response characteristics of GTE dynamic structure are shown on Fig.3. They are obtained in the conditions of structural damping from the impact of the distributed unbalance system of LP rotor.
|
|
|
Fig.3 Steady state response characteristics of the GTE
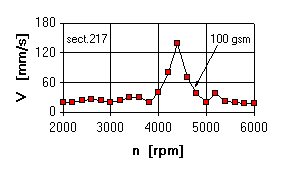
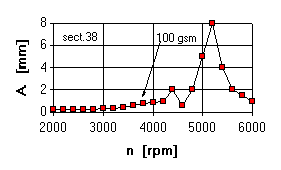
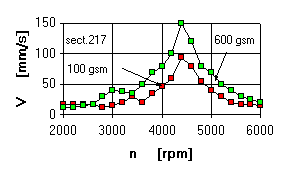
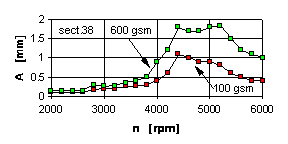
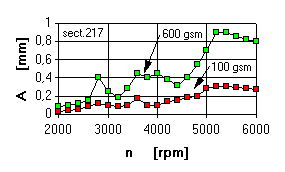
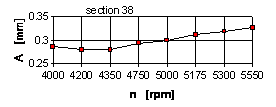
The analysis shows that there are three LP rotor resonance zones, each being coordinated with the zone of increased vibrations obtained in the experiments. In the experiment the main zone of vibrations is in the range of 4250...4500 rpm. Maximum deflections of LP rotor in section 38 (point of rubs) correspond to the mode 5173 rpm.
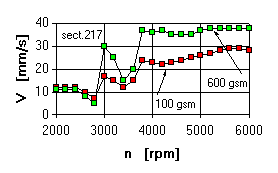
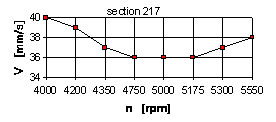
It is noted that in the point of accelerometer adjustment (section 217) the resonance zone corresponding to mode of 5173 rpm was not watched in the experiments.
To simulate the phenomena and define the causes for rubbings of LP rotor turbine shaft and middle pressure rotor in a product we simulated a separate impact of damping on vibrations in the supports of LP rotor.
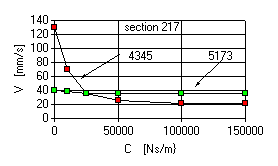
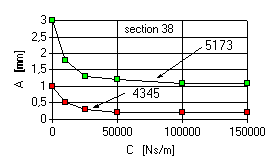
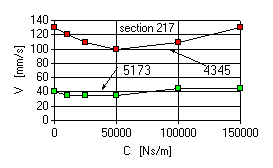
Fig.4,5,6 demonstrate dependencies of the vibration level on damping in the supports for ‘normal’ unbalance distribution. Resonance zones were considered which corresponded to undamped modes 4345 and 5173 rpm.
|
|
|
Fig.4 Vibration sensitivity on front support damping
|
|
|
Fig.5 Vibration sensitivity on intermediate support damping
|
|
|
Fig.6 Vibration sensitivity on rear support damping
The following conclusions have been made.
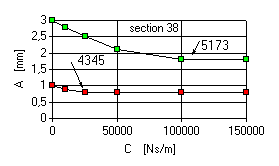
Resonance zone -mode 4345 rpm.
- Damping in the front support exerts considerable effect on the zone, reducing vibrations on the front support (section 217) and LP rotor shaft deflections (section 38).
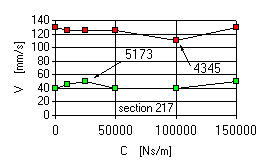
- Damping in the intermediate support slightly reduces vibrations in the front support and deflections of the LP rotor shaft, and beginning from damping coefficient 50000 Ns/m the growth of damping results in the growth of vibration level.
- Damping in the rear support of the LP rotor does not exert any impact on the mode.
Resonance zone -mode 5173 rpm.
- Damping in the front support practically does not influence the vibration level along the front support, lthough reducing the deflections of LP rotor shaft.
- Damping in the intermediate support does not influence the vibration level along the front support, though greatly reducing the deflections of LP rotor shaft.
- Damping in the rear support slightly reduces deflections of LP rotor shaft, exerting no considerable influence on vibrations along the front support.
The dependencies obtained gave also the range of optimal damping coefficients for dampers in the supports. They can be sampled within the range 40000...50000 Ns/m.
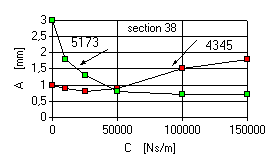
The analysis of forced vibration characteristics obtained for the variants of damping along the front and intermediate supports with different unbalances in section 38 allowed us to outline:
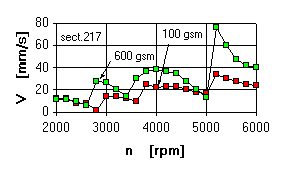
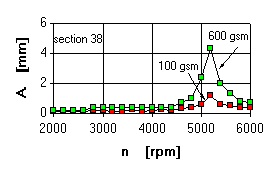
- Damping of the front support of LP rotor is effective, providing increased unbalances of rotor only for mode 4345 rpm. At the mode 5173 rpm the increased unbalance of LP rotor turbine shaft is displayed by a high level of vibration speed (about 80 mm/s) and by a large deflection of the shaft (over 4 mm), Fig.7.
- Damping in the intermediate support of LP rotor is effective for the mode 5173 rpm and it is not for the mode 4345 rpm, Fig.8
- The availability of damping both in the front and in the intermediate support of LP rotor enables us by the increased unbalances to obtain the vibration level along the front support at all modes not higher than 40 mm/s and rotor deflections at the mode 5173 rpm - not greater than 0.9 mm, Fig.9.
|
|
|
Fig.7 Steady state dynamic response of GTE model. C1=50000 Ns/m, C2=0.
|
|
|
Fig.8 Steady state dynamic response of GTE model. C1=0, C2=50000 Ns/m.
|
|
|
Fig.9 Steady state dynamic response of GTE model. C1=50000 Ns/m, C2=50000 Ns/m
The analysis of engine forced vibrations in the linear statement enabled us to make the following general conclusion on rotor contacts. The absence of damping in the intermediate support of LP rotor at the range of 5000...5200 rpm in case of increased unbalance of LP rotor can result in deflections of shaft exceeding the clearance between rotors (4 mm) and, hence, in rotor rubs. Here the LP rotor will perform a synchronous precession, the middle pressure rotor, because of the difference in rotational speeds - non-synchronous one.
DESIGNING OF HYDRODYNAMIC DAMPER OF INTERMEDIATE SUPPORT
In the structure of the intermediate support of LP rotor a damper has been applied which did not provide desirable damping.
To eliminate dangerous vibrations from heat unbalances a new hydrodynamic damper for the intermediate support has been designed. Designing ran in accordance with the procedure developed for practical application [1].
The procedure is based on the use of linear models of GTE dynamic structure and hydrodynamics dampers of different lay-outs with the following estimation of the engine dynamic structure as a non-linear system in the transient analysis. Such an approach allows to get the appropriate time for designing damping devices and obtain good practical results.
The process assumes separate designing of dampers with the tuning of each one for a definite resonance mode.
Among the known lay-outs of dampers we have taken one of the aligned single slot hydrodynamic dampers due to its simplicity and high reliability in operation.
The initial dimensions of a hydrodynamic damper were obtained in the assumption of circular precessions so that under the increased rotor eccentricity around 0.6 the stiffness and damping at the speed 5000...5300 rpm would be optimal, Fig. 10.
|
|
|
Fig. 10 Dynamic characteristics of the hydrodynamic damper for intermediate support
The findings showed that the necessary load-carrying and damping ability could be provided by a hydrodynamic damper made with faced seals with oil supply through holes without a central groove and following geometry: diameter 245 mm, length 40 mm and clearance 0.17 mm.
The final estimation of the engine dynamic response in the nonlinear statement showed that the chosen structure and geometrical dimensions of damper provide the level of vibrations in case of increased unbalance of LP rotor shaft, Fig. 11.
|
|
|
Fig. 11 Dynamic response of GTE nonlinear model with hydrodynamic dampers
LITERATURE
1. M.K.Leontiev, E.V.Borzdyko and S.L.Zvonarev. Gas turbine dynamic response analysis through simulation. Proceedings of the international conference on rotating machine dynamics ROTORDYNAMICS'92. Poster Session Papers. Hotel Des Bains, Venice, Italy, 28-30 April 1992, pp. 1-10.