Back to publications

4. Examples of different damper supports design

4.1 Design of a HD support

Initial Data:

· The damper has piston-type ring seals, uncentralised;

· The damper diameter D=150 mm

· Type of oil MK-22 - dynamic viscosity at 100 OC m=2.05x10-2 Ns/m2

· Required support stiffness E = 0.8o107 N/m;

· Damping N > 15000 Ns/m;

· The rotor operating speed (tuning speed) w = 800 s-1;

· Mass lumped at either of the bearing stations mA = 50 kg

1. Determination of an optimal damper clearance d by recommended gravity parameter.

Assume a value =0.1. Because of WB =mB g the clearance

= (50o9.81)/(50o8002o0.1)=

0.000153 i = 0.153 mm

 

2. The parameter B=0.1 value determines the damper length LR.

LR = =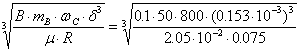

= 0.021 i = 21 mm

3. We choose a sealed damper with oil supplying holes, Fig.11b.

Then the damper can be considered as a "long" one and its length can be estimated as L = LR..

4. The damper performances can be evaluated by approximate dependencies. The analysed damper is not centered, so it is to have some stiffness or bearing ability. So the "p-film" boundary conditions are considered.

For an eccentricity value e=0.4

E = =

=

= 0.214 x109 N/m

C = =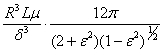

=

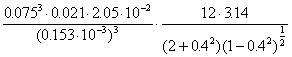= 0.965o106 Ns/m

The obtained values of stiffness and damping are much higher than required (about two orders). So it is impossible to fulful the initial data requirements within the chosen scheme.

5. Another damper scheme is a sealed damper with a central groove, Fig.11e. This damper can be considered as "short" p-film damper with a reduced length L = LR

At eccentricity e = 0.4

E = =

= 0.224 o 107 N/m

C = =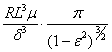

= =

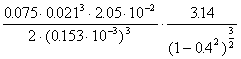= 0.811o104 Ns/m

 

6. To meet initial requirements on stiffness and damping it is possible to increase the damper length in 1.5 times.

NOTE: This calculation is based on Reynolds equations solution for centralised dampers (the rotor weight neglected).

7. If there is available code for nonlinear dynamics analysis it is of use to repeat the calculation at different loading conditions [11].

8. The damper performances are to be checked by testing in a special facility.

Previous Contents Next