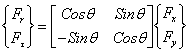Back to publications

3.2.3 Evaluation of HD stiffness and damping

HD dynamic performances can be more accurately evaluated out of hydrodynamic lubrication theory [ Ref. 5 ]. An isoviscous flow in the clearance is described by Reynolds lubrication equations which are resulting out of Navier-Stocks equations at simplifying assumptions:

1) the clearance size is small; 2) the flow is laminar; 3) the oil is incompressible; 4) the oil viscosity is constant; 5) the oil inertia is not considered.

The Reynolds equation is

Here - curcumferential coordinate; - sliding velocity (as usual the damper does not rotate so u=0); h - local oil film thickness.

The equation describes a 2-dimensional flow in axial and circular directions. More accurate equations consider oil inertia, turbulent flow etc, but they need significant computation expences so here are considered only the most influencing factors.

The relationship between the damper parameters and system inertial coordinates (Fig.10) is described by dependencies

then

and

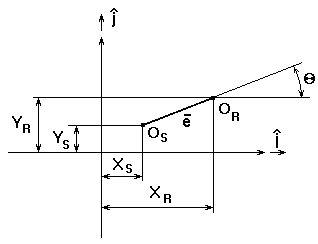
Fig.10 Inertial coordinates

It is of use here to introduce such terms as "short" and "long" dampers similar to "short" and "long" sliding bearings. The Reynolds equation is solved in these terms.

"Long" damper.

For this case the axial pressure distribution is assumed as a parabola producing ends pressure 0.75 of the middle pressure. The pressure function is

“Short" damper

If the end cavitating regions are absent the pressure distribution can be assumed as

These assumptions at u=0 produce out of the Reynolds equations for a "long" damper

and for a "short" damper

These equations can be solved by a finite differences method (FDM). Derivation of the equations above gives

Change of the first and second pressure derivatives to central differences results

and

Rewriting of this equation in each knot of the network in a matrix form results with a system which can be solved under boundary conditions in the oil supply areas [ 5, 16 ].

There are various available models for determination of cavitating regions in the damper . Here we use Reynolds boundary conditions:

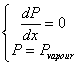
which can be rewritten in FDM knots terms:

?i,k = ?vap, anee ?i,k < Pvap;

Hydrodynamic forces and dynamic coefficients

On the inner damper surface the forces can be determined by integration of the pressure distribution function. The X and Y force components can be determined:

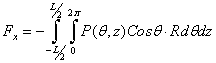
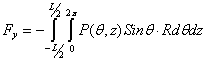
If the pressure distribution within the oil film is known the integration can be performed numerically by Sympson method. The expressions define the forces applied to the rotor. Force gradients or current values of damping and stiffness coefficients are determined:

;

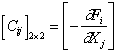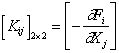
For circular precession the stiffness and damping coefficients can be calculated as following:

;

Here and - radial and tangential components of the hydrodynamical force;

Transmision from unmovable coordinates (X, Y) to rotating coordinates (r, t) is performed by an orthogonal transform:

Previous Contents Next